3 Geometrische Veranschaulichung für drei Varianten

Für v=3 zeigt das Set-Spiel deutliche Analogien zur mehrdimensionalen Geometrie auf: Das Set-Spiel läßt sich mit einem n-dimensionalen Raum vergleichen (siehe 2.5). Jede Eigenschaft stellt dabei eine Dimension dar, und es existieren Analoga zu Geraden, Ebenen und Hyperebenen. Um diese genau zu definieren, haben wir zunächst einen Hilfssatz aufgestellt.

3.1 Hilfssatz I für drei Varianten

Bei drei Varianten bilden drei Karten genau dann ein Set, wenn für jede Eigenschaft gilt, daß die Summe der vorliegenden Varianten durch 3 teilbar ist.
Beweis: Bei zwei verschiedenen Varianten (in bezug auf eine Eigenschaft) weist die setbildende Karte in bezug auf diese Eigenschaft die noch fehlende Variante auf (siehe 2.6). Jede der drei Zahlen 0, 1, 2 kommt daher genau einmal vor, die Summe ist immer 3 und somit durch 3 teilbar. Bei zwei gleichen Varianten (in bezug auf eine Eigenschaft) weist die setbildende Karte in bezug auf diese Eigenschaft ebenfalls diese Variante auf (siehe 2.6). Bei der Summenbildung wird also dreimal die gleiche Zahl addiert, die Summe ist demnach durch 3 teilbar.
Wählt man in einem der beiden Fälle nicht die setbildende Karte, so unterscheidet sich die Karte dementsprechend in mindestens einer Eigenschaft von der setbildenden Karte. In dieser Eigenschaft unterscheidet sich die Variante um 1 oder 2 von der der setbildenden Karte, da nur die Variantenwerte 0, 1, 2 und damit auch nur die Differenzen 0, 1, 2 vorkommen können; eine Differenz von 0 kommt hingegen nur bei Übereinstimmung der Varianten vor. Zwei Zahlen, die sich um 1 oder 2 unterscheiden, können aber nicht beide durch 3 teilbar sein.
Damit ist gezeigt, daß die Summe der Varianten nicht durch 3 teilbar ist, wenn kein Set vorliegt, und daß sie immer durch 3 teilbar ist, wenn ein Set vorliegt. Sie ist also genau dann durch 3 teilbar, wenn ein Set vorliegt.

3.2 Hilfssatz II für drei Varianten

Zu jedem Set {K1, K2, K3} existiert ein Vektor, mit dem man K1 in K2, K2 in K3 und K3 in K1 überführen kann.
Beweis: Man bestimme den Vektor, mit dem man K1 in K2 überführt. Verschiebt man nun K2 um diesen Vektor, so erhält man die setbildende Karte. Sind die beiden Varianten von K1 und K2 nämlich in einer Eigenschaft gleich, so ist die entsprechende Komponente des Vektors 0, die entstehende Karte weist also auch diese Variante auf. Sind die beiden Varianten von K1 und K2 verschieden, ist die entsprechende Komponente des Vektors +1 oder -1, die entstehende Karte weist also die dritte Variante auf. Demnach erfüllt jede Eigenschaft eine der für ein Set erforderlichen Bedingungen, es liegt ein Set vor.
Verschiebt man die so entstandene Karte K3 nochmals um den Vektor, so hat man die Karte K1 insgesamt dreimal um denselben Vektor verschoben, die Summe der einander entsprechenden Komponenten ist durch drei teilbar. Wegen des Modulorechnens ergibt sich also überall insgesamt die Komponente 0, man erhält wieder K1, q.e.d.
Es existieren zu jedem Set zwei Vektoren, die die Bedingung des Hilfssatzes erfüllen, außer dem betrachteten ist das der entgegengesetzte Vektor mit den vom Betrag her gleichen Komponenten.

3.3 Geometrische Definitionen und Zusammenhänge

Unter einer Geraden wird eine Menge von drei Karten verstanden, die ein Set bilden. Da es zu zwei Karten immer genau eine dritte Karte gibt, die mit diesen ein Set bildet, wird eine Gerade durch zwei Karten charakterisiert. Das stimmt mit dem Geradenbegriff der mehrdimensionalen Geometrie überein: Durch zwei verschiedene Punkt läuft auch hier immer genau eine Gerade.
Auch die Parallelität von Geraden wird analog zur mehrdimensionalen Geometrie definiert: Zwei Geraden sind parallel, wenn sie durch eine (Parallel-) Verschiebung ineinander überführt werden können. Eine Verschiebung einer Geraden wird in der Geometrie durchgeführt, indem zu einer oder mehreren Koordinaten jedes Punktes ein Betrag addiert oder subtrahiert wird, der zwar für die unterschiedlichen Koordinaten verschieden sein kann, für die gleichen Koordinaten verschiedener Punkte jedoch identisch ist.
Beim Set-Spiel sind die einzelnen Koordinaten einer Karte die Buchstaben in der Darstellung der Karte als Wort. Verschiebt man nun allerdings eine Karte, müßte man zu jedem Buchstaben einen konstanten Betrag addieren bzw. davon subtrahieren. Tritt dabei ein negativer Wert oder ein Wert >= 2 auf, geht man wie in der Modulorechnung vor: Man betrachtet den natürlichen Rest der Summe beim Teilen durch drei. Dieser ist immer 0, 1 oder 2, es entstehen also immer gültige Karten.
Im Set-Spiel existieren nun pro Koordinate nur drei Möglichkeiten: Entweder man läßt die Koordinate unverändert, man erhöht sie um 1, oder man verringert sie um 1. Die Erhöhung um 2 ist aufgrund der Modulorechnung identisch mit der Verringerung um 1, die Verringerung um 2 ist identisch mit der Erhöhung um 1. Die Komponenten, die zu den einzelnen Eigenschaften beim Verschieben addiert werden, bilden ein Zahlentupel, einen Vektor.
Zwei Geraden sind nun parallel, wenn sie durch eine Verschiebung ineinander überführt werden können, also wenn jede Karte der ersten Geraden einer Karte der zweiten Geraden zugeordnet ist, so daß für jede Eigenschaft n gilt: Addiert man zur n-ten Koordinate der Karte auf der ersten Geraden das n-te Element des Vektors, so erhält man die n-te Koordinate der zugeordneten Karten auf der zweiten Geraden. Dabei muß man natürlich immer modulorechnen.
Verschiebt man eine Gerade zweimal mit demselben Vektor, so bildet jede Karte mit ihren so entstandenen Abbildern Sets. Wird eine Eigenschaft nämlich beim Verschieben nicht verändert, sind die Varianten der drei Karten hier gleich. Wird sie um 1 geändert, tritt die ursprüngliche Variante, die um 1 veränderte Variante und die um 2 veränderte Variante auf, und das sind drei verschiedene Werte. Da bei allen dieser Eigenschaften eine dieser Möglichkeiten eintritt, entsteht ein Set.
Zu einer Karte, die auf einer Geraden liegt und einer Karte, die auf einer dazu parallelen Geraden liegt, liegt die setbildende Karte immer auf der Geraden, die bei erneuter Verschiebung um den vorherigen Verschiebungsvektor entsteht. Wenn es sich nämlich bei der zweiten Karte um ein Abbild der ersten handelt, bildet das zweite Abbild das Set. Ansonsten ist die zweite Karte das erste Abbild einer anderen Karte der Ausgangsgerade. In dem Fall bildet das zweite Abbild der dritten Karte der Ausgangsgerade ein Set: Entweder hat man nämlich eine Eigenschaft bei der Verschiebung nicht geändert, dann sind auch danach noch alle Varianten gleich oder alle verschieden (vorher lag ein Set vor), oder man hat die Variante einer Eigenschaft um 1 in die eine Richtung, die der anderen um 1 in die andere Richtung verändert. Da die Summe der drei Varianten laut Hilfssatz I kongruent 0 mod 3 war und man 1 addiert und 1 subtrahiert hat, ist sie auch jetzt kongruent 0 mod 3, die Varianten der Eigenschaft sind alle gleich oder alle verschieden (Hilfssatz I). Da einer der Fälle bei jeder Eigenschaft vorliegt, liegt also ein Set vor.
Aus diesem Grund sprechen wir auch davon, daß diese drei Geraden, sofern sie unterschiedlich sind, ein Set bilden. Die Menge dieser drei verschiedenen Geraden bezeichnen wir als Ebene. Diese Definition stimmt auch mit der der mehrdimensionsalen Geometrie überein, denn auch da liegen parallele Geraden, die man mit demselben Vektor erzeugt, auf einer Ebene.
Ebenen sind in bezug auf Sets abgeschlossen, das heißt, daß zu zwei beliebigen Karten der Ebene die dritte setbildende Karte auch auf der Ebene liegt: In den Geraden ist das der Fall - sie sind Sets -, und zwischen den Geraden liegt der eben erläuterte Fall vor, der Satz wurde hergeleitet. Liegt ein Set zwischen den Geraden vor, so nennt man es geradenübergreifend.
Auch Ebenen können mit Vektoren verschoben werden, der Begriff der Parallelität gilt genau wie bei Geraden. Nach dem gleichen Prinzip, wie eben durchgeführt, kann man zeigen, daß auch zu zwei Karten zweier paralleler Ebenen die setbildende Karte in einer dritten, um den selben Vektor verschobenen Ebene liegt. Man spricht wieder davon, daß diese drei Ebenen ein Set bilden, die Sets zwischen den Ebenen heißen ebenenübergreifend. Eine Menge von Ebenen, die ein Set bilden, nennt man dreidimensionale Hyperebenen. Auch diese sind in bezug auf Sets abgeschlossen. Analog kann man auch hier die Parallelität und die Aussage "dreidimensionale Hyperebenen bilden Sets" definieren.
Da man das Schritt für Schritt weiterführen kann, definieren wir allgemein:
Unter einer n-dimensionalen Hyperebene wird eine Menge von drei verschiedenen parallelen (n-1)-dimensionalen Hyperebenen verstanden, die ein Set bilden.
Die Parallelität, hyperebenenübergreifende Sets und die Aussage "Hyperebenen bilden Sets" werden dabei definiert, wie es für Geraden, Ebenen und dreidimensionale Hyperebenen schon durchgeführt wurde.

3.4 Einordnung des Set-Spiels in einen affinen Raum

Die geometrische Darstellung des Set-Spiels ist sinnvoll, weil es sich beim Set-Spiel mit n Eigenschaften um einen affinen Raum der Dimension n handelt, wenn man die Menge der Karten als Punktmenge, die Menge der Sets als Geradenmenge und die Beziehung "Karte gehört zu Set" als Inzidenzstruktur auffaßt und die Parallelrelation wie in 3.3 definiert. Wir zeigen zunächst, daß es sich um einen affinen Raum handelt, und dann, daß seine Dimension mit der Eigenschaftszahl des Set-Spiels übereinstimmt.
Laut [7] liegt ein affiner Raum dann vor, wenn folgende Axiome erfüllt sind:

"A1) Zu je zwei verschiedenen Punkten gibt es genau eine Verbindungsgerade."
Diese Bedingung wird vom Set-Spiel erfüllt, da zu zwei beliebigen Karten genau eine setbildende Karte und somit genau ein Set existiert.

"A2) Zu jeder Geraden g und jedem Punkt P gibt es genau eine Gerade l mit P inzident l und g parallel l."
Man kann die Karte P als verschobenes Abbild einer der Karten des Sets g betrachten und den Verschiebevektor bestimmen. Verschiebt man jetzt die beiden anderen Karten des Sets ebenfalls mit diesem Vektor, so hat man ein paralleles Set l. Man kann nun P als Abbild jeder der drei Karten von g ansehen. Ausgehend von einer Karte K₁ kann man die anderen beiden Karten erhalten, indem man eine Verschiebung um einen der Set-Vektoren bzw. den entgegengesetzten Vektor verschiebt. Der Vektor von den beiden Karten zu P ist demnach die Summe aus bzw. und dem Vektor von K₁ zu P. Jede der drei Karten wird also auf das vorherige Abbild der Karte abgebildet, die durch Verschiebung von K₁ mit einem der Setvektoren entsteht, die also auch zu g gehört. Die drei entstehenden Karten sind also die gleichen wie wenn P als Abbild von K₁ angesehen wird. Es gibt also nur ein paralleles Set zu g durch P.

"A3) Ist {A, B, C} ein Dreieck und sind P, Q verschiedene Punkte mit parallel , so schneiden sich die Parallelen durch P und zu durch Q in einem Punkt R."
Beim Verschieben eines Sets ändern sich die Vektoren zwischen zwei Karten nicht. Da parallel zu ist, muß der Vektor also auch einer der Setvektoren des Sets mit A und B sein. Es gilt: 1) oder 2) Unter wird der Ortsvektor des Punktes P verstanden, also ein Vektor, dessen Komponenten den Koordinaten des Punktes P entsprechen. Es gilt: . Nun nehmen wir eine Fallunterscheidung zwischen den beiden Fällen vor:
1. Es ergibt sich bei Addition von :
  
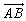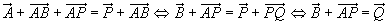
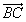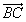  Verschiebt man den Punkt Q um einen der Setvektoren des zu parallelen Sets durch Q, so ergibt sich ebenfalls ein Punkt dieses Sets, er heiße S₁. Da Setvektor jedes zu 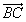parallelen Sets ist, gilt also: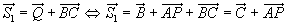
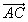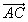  Verschiebt man den Punkt P um einen der Setvektoren des zu parallelen Sets durch P, so ergibt sich ebenfalls ein Punkt dieses Sets, er heiße S₂. Da Setvektor jedes zu 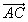parallelen Sets ist gilt also:
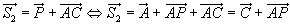
2. Es ergibt sich aus 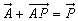durch Subtraktion von :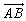
  
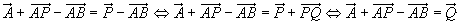
  Da man modulo 3 rechnet, kann man einen beliebigen Vektor auf einer Seite dreifach addieren, ohne daß sich an der Summe etwas ändert. Addiert man links 3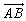, so ergibt sich:
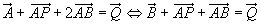
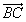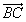  Verschiebt man den Punkt Q nun zweimal um einen der Setvektoren des zu parallelen Sets durch Q, so ergibt sich wiederum ein Punkt dieses Sets, er heiße S₁. Da Setvektor jedes zu 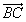parallelen Sets ist gilt also: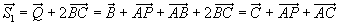
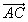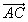  Verschiebt man den Punkt P nun zweimal um einen der Setvektoren des zu parallelen Sets durch Q, so ergibt sich wiederum ein Punkt dieses Sets, er heiße S₂. Da Setvektor jedes zu 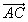parallelen Sets ist gilt also:
In beiden Fällen sind also S₂ und S₁ identisch, es existiert ein Punkt, der sowohl auf dem zu parallelen Set durch Q als auch auf dem zu parallelen Set durch P liegt, diese beiden Sets schneiden sich also in einem Punkt R.

"A4) Auf jeder Geraden liegen mindestens zwei Punkte."
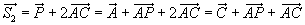
Dieses Axiom ist erfüllt, da jedes Set drei Karten hat.

Da jeder affine Raum eine Basis B hat (vgl. [7]), ist die Dimension eines affinen Raumes als |B|-1 definiert [6]. Nun läßt sich durch vollständige Induktion beweisen, daß die Zahl der Eigenschaften mit der Dimension des Set-Spiels übereinstimmt:
Induktionsanfang: Bei 0 Eigenschaften gibt es nur eine Karte, diese ist ihre eigene Hülle, d.h. die Basis hat die Mächtigkeit 1, somit hat das Set-Spiel die Dimension 0, was mit der Eigenschaftszahl übereinstimmt.
Induktionsschluß: Erweitert man das Set-Spiel um eine Eigenschaft von n auf n+1 Eigenschaften, so geschieht dies, indem man das Set-Spiel mit n Eigenschaften dreimal abbildet, je einmal für jede der drei Varianten. Wenn nun n+1 Karten die Basis für ein n-dimensionales Set-Spiel - also eine dieser Schichten - bildet, so reichen n+1 Karten also nicht als Basis für das n+1-dimensionale Set-Spiel.
Man muß also einen weiteren Punkt hinzufügen, der in einer der anderen beiden Schichten liegt. Die Hülle um die so erweiterte Punktmenge enthält natürlich die Schicht mit den n+1 ausgewählten Karten, aber auch die dritte Schicht, den jede Karte dieser Schicht bildet mit der hinzugefügten Karte und einer Karte der ersten Schicht ein Set. Da wie in jedem Teilraum auch in der Hülle zu je zwei Karten das gesamte Set enthalten sein muß, müssen also alle Karten der dritten Schicht in der Hülle enthalten sein. Die fehlenden Karten der zweiten Schicht bilden mit einer Karte der ersten und einer Karte der dritten Schicht ein Set, müssen also auch zur Hülle gehören. Die Hülle um die n+2 Karten umfaßt also das gesamte Set-Spiel. Da n+1 Karten nicht als Basis ausreichen, umfaßt die Basis also n+2 Karten. Das Set-Spiel mit n Eigenschaften hat also n+1 Dimensionen. So ist ausgehend von 0 der Schluß auf jedes natürliche n möglich.
Das Set-Spiel mit n Eigenschaften und drei Varianten ist also ein affiner Raum der Dimension n.
Da der Raum auf Z₃ⁿ aufgebaut ist, läßt sich die Frage nach der maximalen Kartenzahl ohne Set läßt also geometrisch umformulieren: Wie groß ist die größte Zahl von Punkten eines affinen Raumes über Z₃ⁿ, von denen höchstens zwei auf einer Geraden liegen?

3.5 Hilfssatz III: Verschieben und Vertauschen bei drei Varianten

Bei der geometrischen Darstellung des Set-Spiels handelt es sich lediglich um ein Modell. Das Ziel ist es, Sets durch Geraden in einem n-dimensionalen Würfel geometrisch zu veranschaulichen. Als geometrische Darstellung wurde also ein Darstellungsprinzip gewählt, das diese Bedingung erfüllt. Man kann die Positionen der Punkte im n-dimensionalen Würfel allerdings auch verändern, so daß ebenfalls jedes Set durch eine Gerade dargestellt wird, also eine isomorphe Abbildung vorliegt. Wir wollen jetzt zwei solche Veränderungsmöglichkeiten zeigen, bei denen auch nach der Veränderung eine solche geometrische Darstellung vorliegt:

Zwei parallele (n-1)-dimensionale Hyperebenen werden vertauscht.
Man bildet zwei parallele (n-1)-dimensionale Hyperebenen jeweils auf sich selbst ab, indem man eine um 1 in eine Richtung, die andere um 1 in die entgegengesetzte Richtung verschiebt.

Da eigentlich auch beim Vertauschen der Fall vorliegt, daß eine Ebene in die eine, eine in die andere Richtung verschoben wird, werden die Fälle zusammen betrachtet.
Im folgenden zeigen wir, daß die Veränderungsprinzipien die erforderlichen Bedingungen erfüllen und in den so entstandenen Darstellungen Sets auch weiterhin durch Geraden veranschaulicht werden. Das ist genau dann der Fall, wenn einerseits die Karten jeder Geraden ein Set bilden; andererseits aber drei Karten, die nicht auf einer Geraden liegen, kein Set bilden. Die Karten auf drei Positionen, auf denen vorher Karten lagen, die ein Set bildeten, müssen also auch nach der Veränderung ein Set bilden; die Karten auf drei Positionen, auf denen vorher Karten lagen, die kein Set bildeten, dürfen also auch nach der Veränderung kein Set bilden. Das ist bei den Prinzipien der Fall:
Zum Nachweis betrachten wir nun zunächst ein Set. Lag es vor der Veränderung vollständig in einer der beiden vertauschten bzw. verschobenen Hyperebenen, so wurde es vollständig verschoben und liegt demnach auch weiterhin auf einer Geraden (verschiebt man eine Gerade, so entsteht laut 3.2 eine parallele Gerade).
Lagen die drei Karten vor der Verschiebung nicht in einer Hyperebene, so ist das Set hyperebenenübergreifend, aus jeder der drei parallelen Hyperebenen stammt eine Karte. Man verschiebt jetzt eine der Hyperebenen in die eine, die andere in die andere Richtung. Wird also die Variante einer Eigenschaft bei der Verschiebung nicht verändert, so ist sie auch nach der Verschiebung bei allen drei Karten entweder gleich oder verschieden.
Wird die Variante bei der Verschiebung um 1 verändert, so wird sie bei einer der drei Karten um 1 erhöht, bei einer um 1 vermindert, daß heißt die Summe (modulo 3) bleibt gleich. Da sie laut Hilfssatz I vorher durch drei teilbar war, ist sie es auch jetzt noch. Das wiederum heißt laut Hilfssatz I, daß die Varianten der drei Karten in bezug auf diese Eigenschaft entweder gleich oder verschieden sind.
Da einer dieser Fälle bei jeder Eigenschaft auftreten muß, bilden die drei Karten auch nach der Verschiebung ein Set. Sowohl ein hyperebenenübergreifendes Set als auch ein Set in einer Hyperebene bleibt also ein Set; da es nicht mehr Geraden als vorher sind, symbolisieren also auch alle Geraden Sets.
Beim Verschieben und Vertauschen ändert sich die Zahl der ausgewählten Karten nicht. Auf der Suche nach der Maximalzahl von Karten ohne Set könne Kartenkombinationen, die durch Verschieben und Vertauschen ineinander überführt werden können, also als gleich angesehen werden.

vorheriges Kapitel

nächstes Kapitel

Anregungen, Fragen, Kritik an: Wolf Behrenhoff, Felix Krahmer und Andreas Sorge; Impressum, Datenschutz