7 Untergrenze für drei Varianten
Auf den Set-Internetseiten [3] stellt David van Brink fest, daß sich
bei einer Erhöhung der Zahl der Eigenschaften um 1 die Zahl der Karten,
die man maximal auslegen kann, ohne daß ein Set entsteht, mindestens
verdoppelt und höchstens verdreifacht. Die Begründung hierfür
ist einfach (unter Sn wird hier die maximale Kartenzahl ohne Set im n-dimensionalen
Set-Spiel verstanden):
Wenn wir annehmen, daß das (n+1)-dimensionale Spiel
aus drei n-dimensionalen Hyperebenen besteht, können wir eine Menge
an Karten ohne Set im (n+1)-dimensionalen Spiel konstruieren, die aus zwei
gleichen Hyperebenen, die jeweils die größte setlose Kartenkombination
der vorherigen Dimension enthalten, und einer dritten, leeren Hyperebene
besteht. Weil jedes Set entweder vollständig in einer Hyperebene liegen
muß (das ist nicht möglich, da jede der Hyperebenen entweder
keine Karten oder eine setlose Kombination des n-dimensionalen Spiels enthält)
oder je eine Karte aus jeder Hyperebene enthalten muß (auch das ist
nicht möglich, da die dritte Hyperebene leer ist), haben wir eine
Kombination von 2Sn Karten ohne Set konstruiert.
Angenommen es existiert eine Menge an Karten ohne Set in der (n+1)-ten
Dimension, die 3Sn+1 Karten enthält. Diese Summe aus den Kartenmengen
der drei Hyperebenen muß demnach 3Sn+1 sein. Das bedeutet, daß
eine der Hyperebenen mindestens Sn+1 Karten enthält. Da die größte
Anzahl an Karten ohne Set in dieser Hyperebene aber laut Definition nur
Sn ist, muß hier ein Set vorliegen, und unsere Ausgangsannahme ist
falsch.
Wir haben uns auch mit der Suche nach Untergrenzen beschäftigt und
dabei eine höhere Untergrenze gefunden.
Wir konnten ein rekursives Verfahren entwickeln, mit dem man in einem
n-dimensionalen Set-Spiel - ohne ein Set zu erhalten - ein oder zwei Karten
mehr auswählen kann als mit dem Prinzip der bloßen Verdopplung
der (n-1)-dimensionalen Lösung - bei ungeraden n kann eine, bei geraden
n können zwei Karten mehr als beim bloßen Verdoppeln belegt
werden. Die nach diesem Prinzip entstehenden Kartenanordnungen nennen wir
Umaxkombination (Umax=Untergrenze für die Maximalzahl auslegbarer
Karten ohne Set).
Dazu geht man von einem n-dimensionalen Set-Spiel mit ungeradem n aus.
Zwei (n-1)-dimensionale Hyperebenen seien bekannt, in denen je eine Umaxkombination
von Karten enthalten ist - diese Hyperebenen heißen M1
und M2 - und die folgende Charakteristika aufweisen (unter einer
1-Hyperebene wird eine (n-1)-dimensionale Hyperebene verstanden, die in
der geometrischen Darstellung in der Ebene nur rechts unten eine Karte
hat):
-
Zwischen zwei 1-Hyperebenen und einer M1 bzw. M2-Hyperebene
existiert kein Set.
-
Zwischen je einer M1- und M2-Hyperebene und einer
1-Hyperebene existiert kein Set.
Eine Umaxkombination für das n-dimensionale Set-Spiel wird nun aus
einer M1-, einer M2- und einer 1-Hyperebene gebildet.
Hier existiert laut Voraussetzung kein Set.
Auch für ein (n+1)-dimensionales Set-Spiel kann man aus M1-Hyperebenen,
M2-Hyperebenen und 1-Hyperebenen eine Umaxkombinationen konstruieren;
hier ist sogar die Konstruktion von zwei Umaxkombinationen möglich,
die die Voraussetzungen für M1 und M2 erfüllen
(siehe Abbildung 8) und es somit ermöglichen, den Rekursionsschritt
nochmals durchzuführen.
| M1 |
M2 |
1 |
:=M1 |
1 |
1 |
M2 |
:=M2 |
0 |
0 |
0 |
:=1 |
| M2 |
M1 |
1 |
1 |
1 |
M2 |
0 |
0 |
0 |
| 1 |
1 |
0 |
M1 |
M1 |
0 |
0 |
0 |
1 |
Abbildung 8: Die Konstruktionsvorschrift
für M1, M2 und 1
Jedes Kästchen (nicht jeder 3x3-Kasten!) steht hier für
eine (n-1)-dimensionale Hyperebene. Setzt man an die Stelle eines Kästchens
die jeweilige Hyperebene, so ergibt sich die geometrische Darstellung in
der Ebene; 0 steht hierbei für eine Hyperebene ohne Kartenbelegung.
Um nachzuweisen, daß es sich wieder um Umaxkombinationen handelt,
muß man zeigen, daß in ihnen kein Set vorliegt.
Die einzelnen (n-1)-dimensionalen Hyperebenen beinhalten kein Set (siehe
Voraussetzung für M1 und M2; 0 und 1 enthalten
zu wenig Karten). Zwischen den Hyperebenen kann nur ein Set vorkommen,
wenn die Hyperebenen in der obigen Darstellung in Kästchen liegen,
die im zweidimensionalen Set-Spiel ein Set bilden würden. In welchem
Kästchen eine Hyperebene liegt, hängt nämlich auch von zwei
Eigenschaften ab, und die Varianten in bezug auf diese müssen natürlich
auch jeweils entweder gleich oder verschieden sein.
Ein Set kann jetzt nur vorliegen, wenn entweder unter diesen drei Hyperebenen
zwei M1-, zwei M2- oder drei 1-Hyperebenen vorkommen.
Als weitere Kombinationen aus den vorhandenen Hyperebenen M1,
M2, 1 und 0 kommen nur Kombinationen aus einer M1
bzw. M2 und zwei 1-Hyperebenen, die Kombination aus je einer
M1- und M2- sowie einer 1-Hyperebene und Kombinationen
mit einer 0-Hyperebene in Frage. Diese Kombinationen enthalten entweder
per Definition kein Set, oder sie enthalten eine 0-Hyperebene; dann liegt
zwischen ihnen ebenfalls kein Set vor.
Bei beiden Umaxkombinationen liegt kein Set vor, denn sowohl die setbildende
Hyperebene zu den beiden M1-Hyperebenen als auch die setbildende
Hyperebene zu den beiden M2-Hyperebenen ist 0 und enthält
somit keine Karte. Drei 1-Ebenen liegen ebenfalls in keinem der beiden
Fälle so, daß sie ein Set bilden, denn sie sind wie die Karten
in 41 bzw. 42 (siehe Abbildung 9) angeordnet, und
dort existiert bekanntlich kein Set.
| X |
X |
- |
:=41 |
- |
- |
X |
:=42 |
- |
- |
- |
:=1 |
| X |
X |
- |
- |
- |
X |
- |
- |
- |
| - |
- |
- |
X |
X |
- |
- |
- |
- |
Abbildung 9: Ausgangsstellung der Rekursion
und Maximallösung für n=3
Es handelt sich also in beiden Fällen um Umaxkombinationen. Damit
sie aber für M1 und M2 eingesetzt werden können,
müssen sie die oben angegebenen Bedingungen erfüllen:
-
Zwischen zwei 1-Hyperebenen und einer M1 bzw. M2-Hyperebene
existiert kein Set.
Das ist hier der Fall, denn ein Set zwischen den Hyperebenen müßte
die beiden in den 1-Hyperebenen belegten Felder beinhalten, deren setbildendes
Feld ganz rechts unten in der M1- bzw. M2-Hyperebene
ist jedoch frei - es liegt in der 0-Hyperebene (vgl. Abbildung 8).
-
Zwischen einer M1-, einer M2- und einer 1-Hyperebene
darf kein Set entstehen.
Diese Bedingung ist ebenfalls erfüllt, denn auch ein hyperebenenübergreifendes
Set kann nur zwischen drei (n-1)-dimensionalen Hyperebenen entstehen, wenn
unter ihnen zwei M1-, zwei M2- oder drei 1-Hyperebenen
vorhanden sind. Drei 1-Hyperebenen bilden hier aber kein Set, weil sie
auf Positionen liegen, die im dreidimensionalen Setspiel kein Set bilden
(vgl. die Lage der 1-Hyperebenen (Abbildung 8) und die Lage der Karten
im dreidimensionalen Setspiel (Abbildung 9)).
Wären zwei M1- bzw. M2-Hyperebenen am Set
beteiligt, so müßten diese mit der 1-Hyperebene rechts unten
in der dritten (n+1)-dimensionalen Hyperebene ein Set bilden. Betrachtet
man aber diese und alle (n-1)-dimensionalen M1- und M2-Hyperebenen,
so liegen diese wiederum an Positionen, die im dreidimensionalen Set-Spiel
kein Set bilden. Es kann also keine zwei M1- oder M2-Hyperebenen
geben, die mit der 1-Hyperebene ein hyperebenenübergreifendes Set
bilden.
Hiermit ist auch diese Voraussetzung erfüllt.
Man kann also mit den nach diesem rekursiven Prinzip erhaltenen Umaxkombinationen
einen weiteren Rekursionsschritt durchführen, ohne daß ein Set
entsteht. Den Ausgangspunkt für die Rekursion bildet die in Abbildung
9 dargestellte Maximallösung für n=3. Die Ebenen 41
und 42 erfüllen die Voraussetzungen für M1
und M2. So läßt sich von n=2 auf n=3 und n=4, aus
den so entstandenen Lösungen für n=4 auf n=5 und n=6 und damit
auf alle natürlichen Zahlen >=3 schließen.
Erzeugt man die Umaxkombination bei einem ungeraden n, so fügt
man zusätzlich zum Verdoppeln eine Karte hinzu, denn in zwei Hyperebenen
liegt jeweils eine Umaxkombination für n-1 vor; die Karte der 1-Hyperebene
kommt hinzu.
Erzeugt man die Umaxkombination bei einem geraden n, so fügt man
zusätzlich zum Verdoppeln zwei Karten hinzu. In M1 (Abbildung
8) liegen nämlich in den Hyperebenen, die die oberen beiden Reihen
bilden, Umaxkombinationen für n-1 vor; in der Hyperebene, die die
untere Reihe bildet, liegen zwei Karten. M2 besteht aus den
gleichen Hyperebenen wie M1 und beinhaltet daher auch genauso
viele Karten.
Will man nun berechnen, wie viele Karten eine Umaxlösung für
n Eigenschaften enthält, so geht man von einer Ebene mit vier Karten
(n=2) aus und führt die Rekursionsvorgänge nacheinander aus.
Die Kartenzahl wird dabei immer verdoppelt, wobei abwechselnd 1 und 2 addiert
wird. Es ergibt sich also folgende Formel:
(((4·2+1)·2+2)·2+1...)·2+2 für gerade
n und
(((4·2+1)·2+2)·2+1...)·2+1 für ungerade
n,
denn der letzte Summand gibt die im letzten Rekursionsschritt addierte
Kartenzahl an.
Die Formel für gerade n läßt sich nun vereinfachen:
Die 4 wird mit jeder Erhöhung der Eigenschaft um 1 mit 2 multipliziert.
Da die erste Verdopplung beim Schritt von n=2 auf n=3 ist, wird die 4 genau
n-2 Mal verdoppelt. Der erste Summand im Endergebnis ist also 4·2n-2=2n.
Die 1, die nach dem Verdoppeln der 4 addiert wird, wird einmal weniger
verdoppelt, es ergibt sich 1·2n-3. Die 2, die nach dem
zweiten Verdoppeln addiert wird, wird noch einmal weniger verdoppelt, es
ergibt sich 2·2n-4=2n-3. Dieser Summand ist
also doppelt vorhanden. Es ergibt sich insgesamt 2·2n-3=2n-2.
Die nächste 1 und die nächste 2 werden jeweils zweimal weniger
verdoppelt, es ergibt sich als Summand 2n-4. Dies kann man nun
weiterführen; bei der letzten 1 und der letzten 2 entsteht der Summand
22. Insgesamt entsteht also folgende Summe:
2n+2n-2+2n-4+...+22
=22·(n/2)+22·(n/2-1)+22·(n/2-2)+...+22·1
=4n/2+4n/2-1+4n/2-2+...+41
=sum(4k, k=1..n/2)
Diese Summe läßt mit Hilfe der expliziten Formel für
geometrische Reihen vereinfachen:
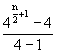 =
=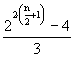 =
=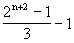
Den Term für ungerade n erhält man, indem man den Term für
n-1 (n-1 ist gerade) verdoppelt und 1 addiert:
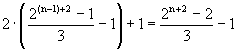
Sowohl der Term für gerade als auch der für ungerade n und
demnach auch ihre ersten Summanden sind ganze Zahlen. Die ersten Summanden
sind nun um 1/3 bzw. 2/3 kleiner als (2n+2)/3 und somit gleich
der größten ganzen Zahl, die kleiner als (2n+2)/3
ist. In beiden Formeln kann man also für den ersten Summanden 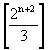 einsetzen. Damit ergibt sich für gerade und ungerade n dieselbe Formel.
einsetzen. Damit ergibt sich für gerade und ungerade n dieselbe Formel.
Man kann daher bei n Eigenschaften (n>=3) immer 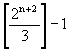 Karten auswählen, ohne daß ein Set entsteht.
Karten auswählen, ohne daß ein Set entsteht.
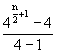 =
=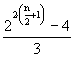 =
=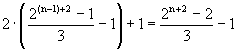
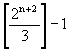 Karten auswählen, ohne daß ein Set entsteht.
Karten auswählen, ohne daß ein Set entsteht.